최단경로:
하나의 정점에서 다른 모든 정점까지(Single-source Shortest Path Problem)

- 시작점 v에서 G의 나머지 모든 정점까지의 최단 경로
- 시작점 v와 목표점 t까지의 경로 중, 경로를 구성하는 간선들의 가중치 합이 최소가 되는 경로
- 방향 그래프 G = (V, E), weight[l, j] >=0
Dijkstra 최단 경로 알고리즘
Dijkstra 최단 경로 알고리즘의 원리
- S: 최단 경로가 발견된 정점들의 집합
- weight[i, j]: 간선 <i, j>의 가중치
- Dist[i]: S에 속하지 않은 i에 대해서, v에서 시작하여 S에 있는 정점만을 거쳐 정점 i에 이르는 최단 경로의 길이
- 처음 S에는 시작점 v만 포함, Dist[v] = 0
- 가장 최근에 S에 첨가된 노드를 u라고 하자.
- u의 모든 인접 정점 w에 대해 Dist[w]를 다시 계산
- S에 포함되지 않은 w중에서 dist[w]가 가장 작은 w를 S에 첨가
- 모든 정점에 대한 최단 경로가 결정될 때까지 2~4번 반복

- ShortestPath 함수 - 최단 경로의 길이 결정
void MatrixWdigraph::ShortestPath(const int n, const int v){
for(int i = 0; i < n; i++){
s[i] = false;
dist[i] = length[v][i];
}
s[v] = true;
dist[v] = 0;
for (i = 0; i < n-2; i++){
int u = Choose(n);
s[u] = true;
for(int w = 0; w < n; w++)
if(!s[w] && dist[u] + length[u][w] < dist[w])
dist[w] = dist[u] + length[u][w];
}
}* 수행시간: O(n^2)
모든 간선의 비용이 양수일 때는 다익스트라 최단 경로의 알고리즘을 사용하면 된다.
- 음의 가중치가 허용된 최단 경로

Bellman and Ford 알고리즘
Dist^k[u]: 시작점 v에서 정점 u까지 최대 k개의 간선을 갖는 최단 경로의 길이
- Dist^1[u] = wieght[v, u]
- Dist^(n-1)[u]: 시작점 v에서 정점 u까지의 최단 경로의 길이
만일 시작점 v에서 어떤 정점 u까지의 최단 경로가 최대 k개까지의 간선을 포함할 수 있는 경우에서
- k-1개 이하의 간선만 포함: Dist^[u] = Dist^(k-1)[u]
- k개 간선을 포함: 시작점 v에서 정점 u에 인접한 어떤 정점 i까지의 최단 경로를 포함하므로, Dist^k[u] = min{Dist^(k-1)[i] + weight[i, u]}

void MatrixWDigraph::BellmanFord(const int n, const int v){
for(int i = 0; i < n; i++)
dist[i] = length[v][i];
for(int k =2; k <= n-1; k++)
for(each u such that u != v and u has at least one incoming edge)
for(each <i, u> in the graph)
if(dist[u] > dist[i] + length[i][u])
dist[u] = dist[i] + length[i][u];
}인접 행렬 사용 시: O(n^3)
인접 리스트 사용 시: O(ne)
벨만포드 알고리즘은 다익스트라 알고리즘에 비해 느리다.
모든 정점 쌍의 최단 경로(All-pairs Shortest-path Problem)
- 하나가 아닌 모든 정점을 시작점으로 하는 최단 경로
- 각 정점을 시작점으로 n번 shortestpath 알고리즘 사용
- 음이 아닌 가중치: O(n^3)
- 음의 가중치를 허용하면: O(n^4)
- 음의 가중치를 가진 그래프의 모든 쌍에 대한 최단 경로를 O(n^3)에 찾을 수 있는 알고리즘
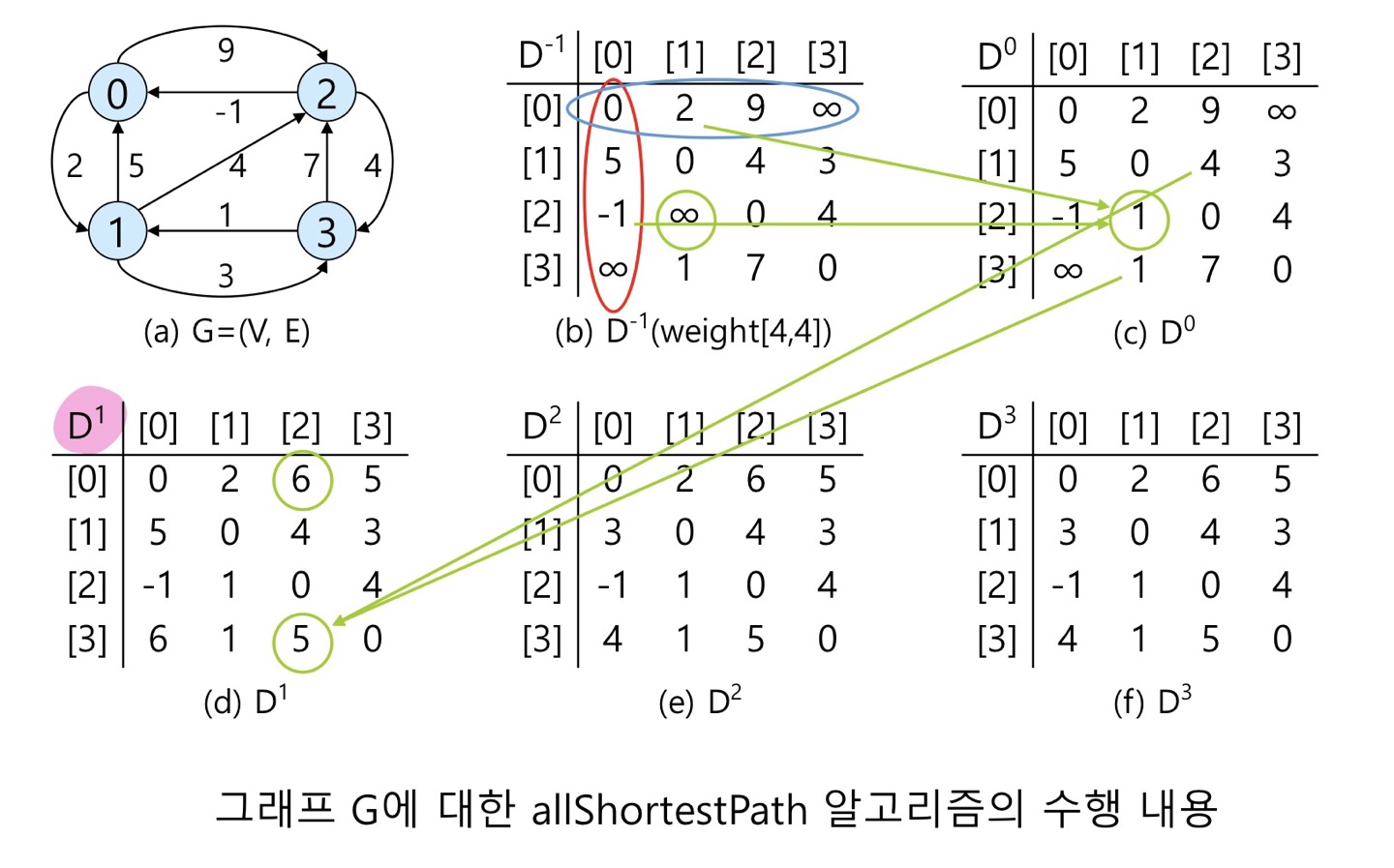
void MatrixWDigraph::AllLengths(const int n){
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
a[i][j] = length[i][j];
for(int k = 0; k < n; k++)
for(i = 0; i < n; i++)
for(int j = 0; j < n; j++)
if((a[i][k] + a[k][j]) < a[i][j])
a[i][k] + a[k][j];
}'2-1 학기 > Data Structure' 카테고리의 다른 글
| [자료구조] 해싱(Hashing) (0) | 2023.06.16 |
|---|---|
| [자료구조] 정렬(Sort) (0) | 2023.06.06 |
| [자료구조] 최소 비용 신장 트리(Minimum-cost Spanning Tree) (1) | 2023.05.29 |
| [자료구조] 그래프 순회(Graph Traversal) (0) | 2023.05.29 |
| [자료구조] 그래프(Graph) (0) | 2023.05.29 |


